Given, a complicated darlington circuitry:

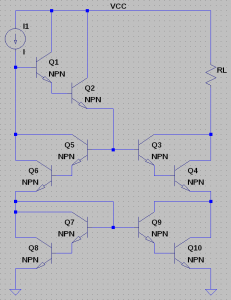
We now replace the darlington pairs with single NPN transistors by defining: $$I_C=I_B \cdot a$$ with $$a=(\beta+1)\cdot\beta$$ and $$I_E=I_B \cdot b$$ with $$b=(\beta+1)^2$$

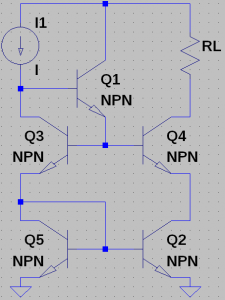
Now we set:
$$I_{KD} = I_{B1} + I_{C3} = I_{B1} + I_{B3} \cdot a$$ and $$I_{RL}=I_{C4}=I_{B4}\cdot a$$ and $$I_{B2}=I_{B5}$$ and $$I_{KD} + I_{C1} + I_{RL} = I_{E5} + I_{E2} $$
$$I_{KD} + I_{B1} \cdot a + I_{RL} = I_{B5} \cdot b + I_{B2} \cdot b = 2\cdot I_{B5}\cdot b = 2\cdot I_{B2}\cdot b$$
$$\Rightarrow I_{RL}=- a \cdot I_{KD} – I_{KD} + a^2 \cdot I_{B3} + 2 \cdot b \cdot I_{B2}$$

And resolve the current equation:
$$I_{B3} \cdot b = I_{E3} = I_{C5}+I_{B2}+I_{B5}$$
$$=I_{C5}+2 \cdot I_{B2}$$
$$=I_{C5}+2 \cdot I_{B5}$$
$$=a \cdot I_{B5}+2 \cdot I_{B5}=(a+2)\cdot I_{B5}=(a+2)\cdot I_{B2}$$

$$\Rightarrow I_{B2} = I_{B5} = \frac{1}{a+2} \cdot I_{E3} =\frac{b}{a+2} \cdot I_{B3}$$
$$I_{E1} = I_{B1} \cdot b = I_{B3}+I_{B4}$$

$$I_{C2} = I_{B2} \cdot a$$
$$= I_{E4}=I_{B4} \cdot b$$
$$\Rightarrow I_{B4} = \frac{a}{b}\cdot I_{B2}=\frac{a}{b}\cdot\frac{b}{a+2} \cdot I_{B3}$$

$$I_{RL}=\frac{a^2 b}{a^2 b + 2 a b +2}$$