Hi
I’m working on a python script which uses a cascaded triangular arbitrash in order to multiply money.
But so far the calculations seem to be all unsatisfying.

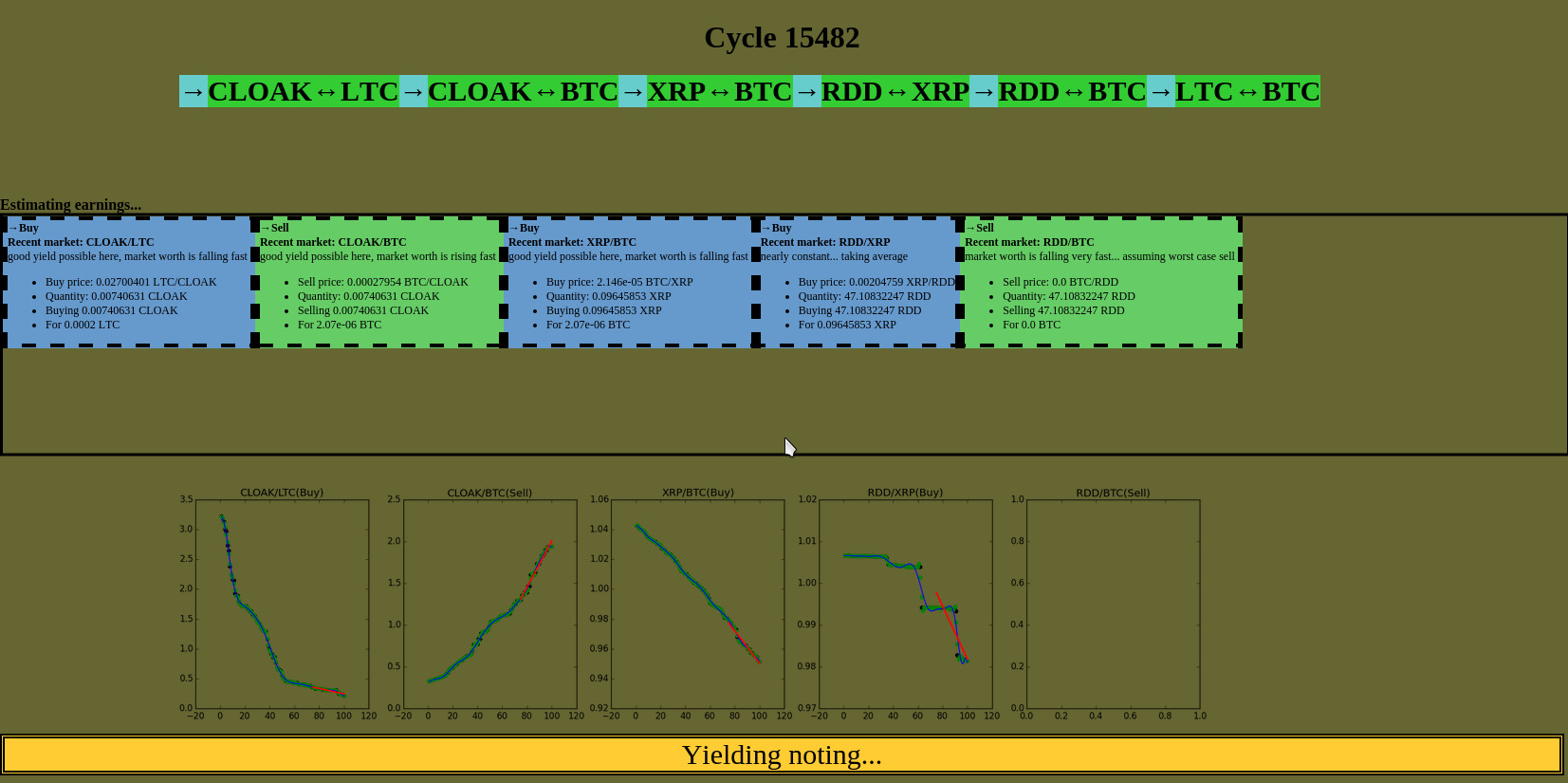
What I’m doing so far is fetching and filtering and interpolating the values in order to estimate the trade development:

#!/usr/bin/python
import sys
import os
import copy
import math

# delays:
from time import sleep

# web api
from Cryptsy import Api

#plotting the stuff
import matplotlib
matplotlib.use("TkAgg")
from matplotlib.pyplot import plot
from matplotlib.pyplot import figure
from matplotlib.pyplot import close
from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg, NavigationToolbar2TkAgg
from IPython import display

#numpy stuff:
from numpy import delete
from numpy import array
from numpy import linspace
from numpy import polyfit
from numpy import poly1d
from numpy import newaxis
from numpy import ones

#scipy stuff
from scipy.signal import wiener
from scipy.optimize import curve_fit
from scipy.ndimage.filters import convolve1d
from scipy.interpolate import interp1d
from scipy.interpolate import InterpolatedUnivariateSpline
from scipy.signal import wiener
from scipy.signal import gaussian
from scipy.signal import savgol_filter

#sklearn
from sklearn.gaussian_process import GaussianProcess
from sklearn.linear_model import LinearRegression
from sklearn.isotonic import IsotonicRegression
from sklearn.cross_validation import cross_val_predict
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.utils import check_random_state

#pyqt fit
from pyqt_fit import npr_methods
import pyqt_fit.nonparam_regression as smooth

…

	x = linspace(1, len(price_array), len(price_array))
	y = array(price_array)
	filtered_y = savgol_filter(y, window_length, savgol_filter_polyorder)

	k0 = smooth.NonParamRegression(x, filtered_y, method=npr_methods.LocalPolynomialKernel(q=gauss_poly_deg))
	k0.fit()
	z = k0(x)

	avg_diff_number=len(x)/4

	new_x=x[len(x)-avg_diff_number-1:]
	new_z=z[len(z)-avg_diff_number-1:]
	clf = LinearRegression()
	clf.fit(new_x[:,newaxis],new_z)
	tangent=clf.predict(new_x[:,newaxis])

	num_different=(tangent[-1]-tangent[0])/(new_x[-1]-new_x[0])

If someone has a better idea: Please say so!